Применение закона Фиттса в дизайне и проектировании интерфейсов

В результате эксперимента ученый выявил интересную закономерность: чем больше расстояние и чем меньше размер до цели, тем больше времени требуется для ее достижения.

Именно этот принцип и лег в основу закона. И хотя с момента его открытия прошло уже более 60 лет, сегодня закон Фиттса активно применяется в проектировании и дизайне интерфейсов. Об этом мы сейчас и поговорим.

Суть эксперимента

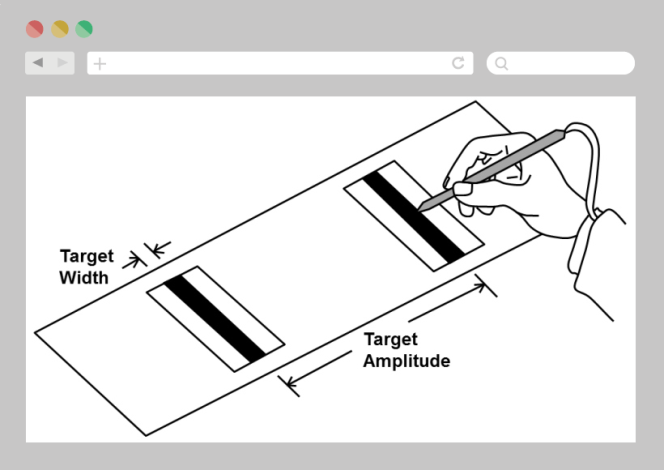
На горизонтальной плоскости расположены две цели-полоски одинаковой ширины. Человек по очереди касается каждой полоски. Задача — попасть в каждую цель как можно быстрее.

Меняя ширину целей и расстояние между ними, Пол Фиттс замерял время, которое требовалось для точного попадания в цели. Он выявил закономерность, которую, в свою очередь, описал математической формулой.

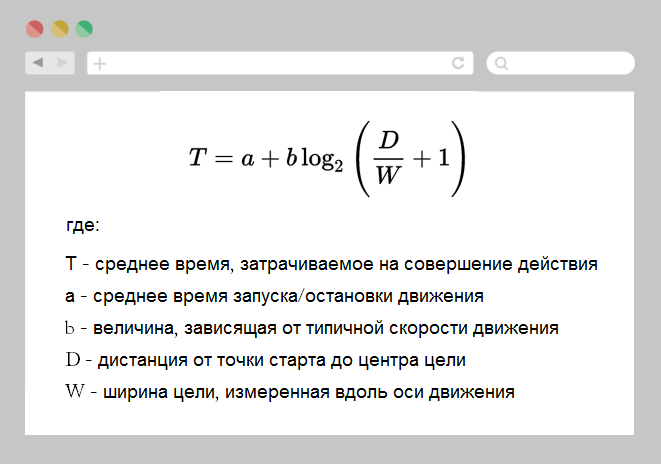
Формула и расшифровка по материалам Википедии.

В упрощенном виде формулу можно объяснить так: общее время достижения цели зависит от скорости движения и ширины цели вдоль оси движения.

Коэффициенты a и b при этом будут постоянны в зависимости от индивидуальных особенностей человека и ситуации, в которой происходит взаимодействие с целью.

Обратите внимание: Фиттс исследовал однонаправленные движения, которые совершались вдоль одной оси. Именно по этой причине высота цели значения не имеет при перемещении между ними по горизонтальной оси.

Сам процесс достижения цели при этом можно разделить на несколько этапов:

1. Локализация — время описывается коэффициентом a.

2. Движение — непосредственно перемещение к цели.

3. Торможение — снижение скорости движения перед достижением цели.

4. Достижение — касание.

Что все это значит

1. Чем больше цель — тем проще и быстрее можно ее достигнуть.

2. Даже небольшое увеличение маленькой цели существенно увеличить скорость ее достижения.

3. Но после определенного этапа увеличение цели практически не отражается на скорости ее достижения.

Объясняются эти выводы логарифмической зависимостью между переменными. Давайте этот момент немного поясним. Вот график нашей функции, который описывает зависимость между размером цели и временем ее достижения при неизменной дистанции:

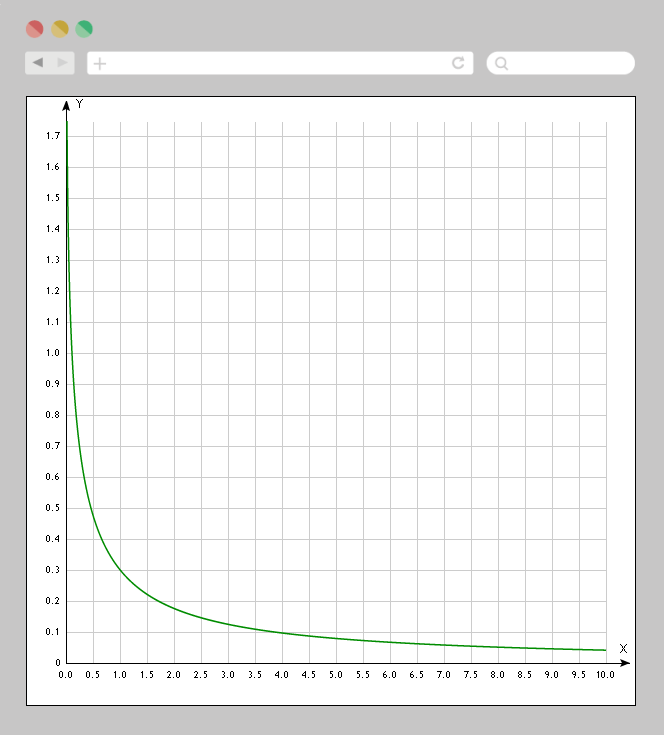
Ось Х — это размер нашей цели. Ось У — время.

Мы видим, что до определенного момента даже небольшое увеличение размера дает существенное сокращение времени. Например, при увеличении размера с 0,5 до 1 время сокращается с 0,45 до 0,3, т.е. примерно на 30%.

Но чем больше мы увеличиваем размер, тем незначительнее сокращается время достижения цели. Обратите внимание, при увеличении размера с 8 до 10 время достижения уже почти не меняется.

Как закон Фиттса применяется в дизайне

При создании дизайна и проектировании интерфейса закон Фиттса помогает определить оптимальные размеры и взаимное расположение кнопок, ссылок и других элементов на странице в зависимости от того, чего именно мы хотим добиться от пользователя.

Также закон позволяет задать оптимальные для пользователя зоны нажатия для всех кликабельных элементов интерфейса.

Но здесь нужно учитывать важную особенность: Фиттс проводил исследования для движения строго слева направо. Стартовая точка при этом находится над одной из целей. В реальных же условиях стартовая точка может быть где угодно, а оптимальная ширина в одном измерении может быть не совсем оптимальной в другом.

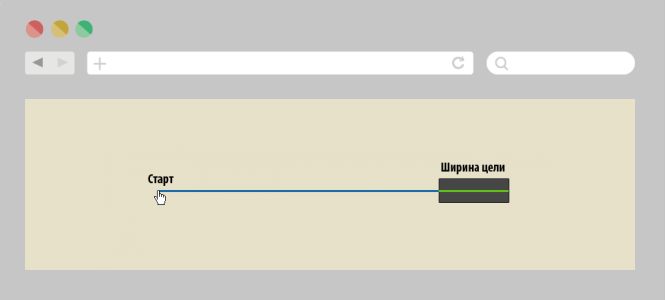
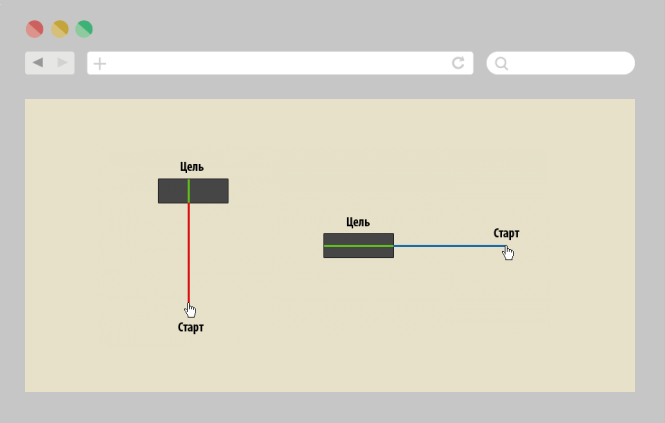
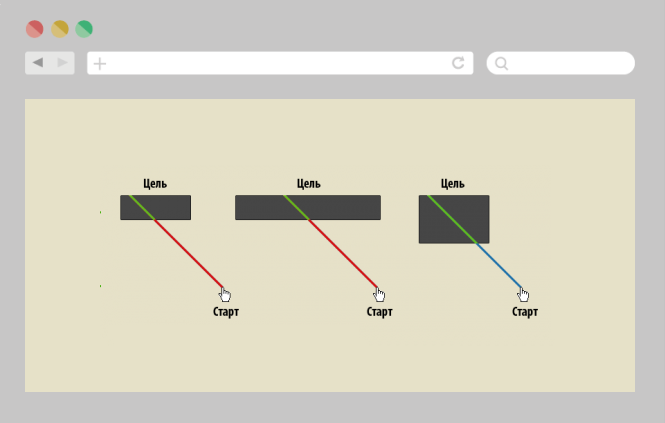
Еще одна особенность, характерная для применения закона Фиттса в веб-разработке и в разработке приложений, — это появлений зон бесконечной ширины.

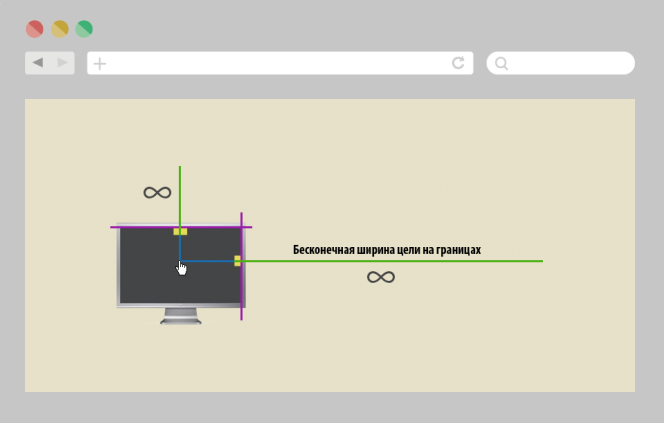
В силу того, что экран ограничен по размерам, элементы, которые находятся на границах имеют условно бесконечную ширину, потому что курсор при попытке в них попасть просто упрется в край экрана и нам не нужно дополнительное время на то, чтобы попасть в элемент по ширине.

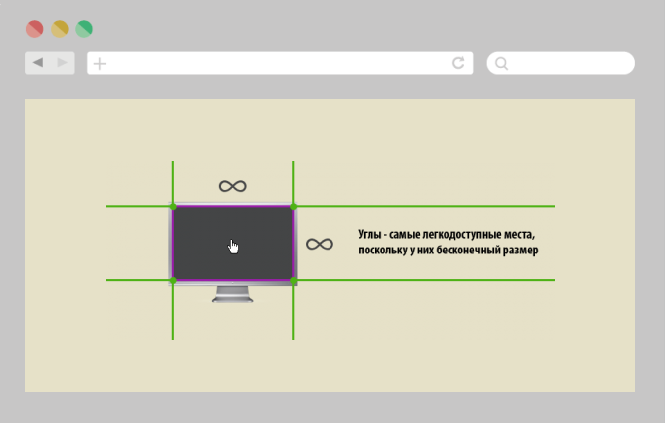
Углы в вебе бесконечны — мы можем моментально передвинуть курсор в любой угол, не обращая внимания на реальные размеры элемента, и все равно в него попадем.

Примеры

Нижняя панель в старых версиях Windows, в нашем случае это XP, спроектирована в соответствии с законом Фиттса.

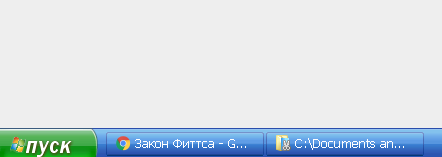
Кнопка «Пуск» расположена в нижнем левом углу экрана — это бесконечная зона, в которую легко попасть за минимальное время с любой стартовой позиции.

Вкладки приложений при этом по ширине практически совпадают с самой нижней панелью, что делает попадание в них также достаточно простым практически с любой позиции.

Обратите внимание, ширины вкладок достаточно, чтобы на них помещался логотип приложения и часть заголовка. Это сокращает время на определение направления движения и локализацию цели.

В новой версии, Windows 10, бесконечный угол остался, но вкладки стали не такими широкими.

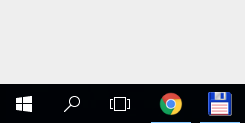
Если мы перейдем в правый верхний угол, можно увидеть еще один интересный пример воплощения закона.

Хотя кнопка закрытия браузера достаточно маленькая и на несколько пикселей отстоит от края экрана, зона нажатия расширена до угла. Курсор точно так же легко, как и с «Пуском» можно, практически не целясь, поместить в верхний правый угол и закрыть приложение.

В новой версии операционной системы зона нажатия совпадает с границами элемента. Но при этом угол по-прежнему остается бесконечным.

Пример использования бесконечной ширины по бокам экрана мы можем наблюдать на сайте практически любой компании.

Вкладка «Оставить заявку», онлайн чат, иногда кнопки социальных сетей — размещение этих элементов по краям экрана позволяет сократить время, необходимое для достижения цели.

Илья Бирман приводит примеры использования закона Фиттса при проектировании зон нажатия в меню.

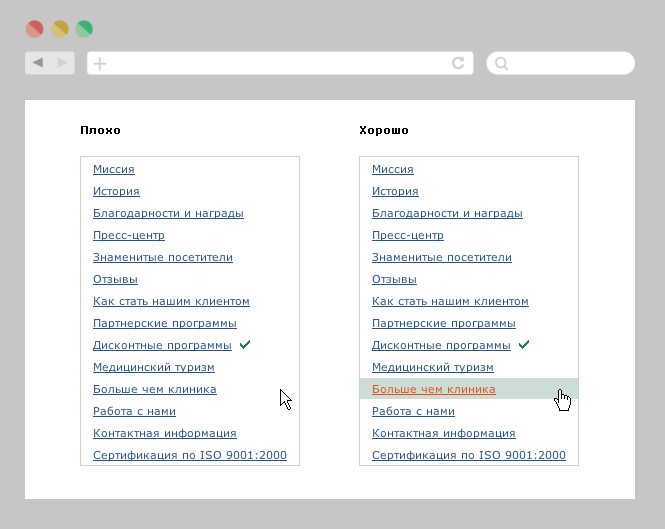
В плохом варианте кликнуть можно только по ссылке, в правильном — по всей ширине элемента вокруг ссылки. За счет расширения зоны кликабельности уменьшается время на достижение цели.

Еще один интересный пример — расширение зоны кликабельности для контекстных ссылок при просмотре сайта со смартфона.

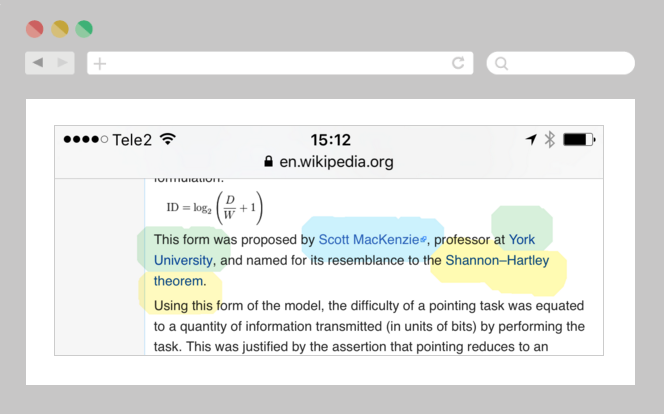
Попасть в нужную ссылку становится намного проще, чем при использовании стандартного сценария, который предполагает нажатие только на текст ссылки.

Выводы и рекомендации

• Закон Фиттса одинаково применим при проектировании как веб, так и мобильных интерфейсов.
• Также закон показывает одинаковые результаты вне зависимости от того, курсором или пальцем производится движение в направлении цели.
• Закон помогает определить оптимальные размеры кнопок и других элементов, продумать наиболее удобные для пользователя варианты их размещения в интерфейсе.
• Грамотное использование бесконечных углов и зон бесконечной ширины по краю позволяет увеличивать кликабельность элементов без увеличения их фактической видимой ширины.

Тестирование интерфейса или продукта на реальных пользователях позволяет выявить несоответствие закону Фиттса. Узнать стоимость юзабитили-аудита и заказать его можно на сервисе AskUsers.

Если среди замечаний респондентов вы увидите упоминания о неудобных ссылках, невозможности нажать на какие-то элементы, а системы веб-аналитики при этом фиксируют большое количество ошибочных переходов на нецелевые страницы, это четко свидетельствует о том, что пора всерьез заняться интерфейсом и привести его к общепринятым стандартам юзабилити.